This is a mathematical problem that took almost 100 years to solve

At some point in our lives, we’ve all been in a situation where we’re looking at a math test that seems impossible to solve. What if it took almost a century to find a solution to a problem?

to Mathematicians deal with Ramsey theoryThis is largely the case. In reality, Little progress has been made in resolving Ramsay’s problems since the 1930s.

Now, researchers at UC San Diego Jack Verstraete and Sam Matthews have found the answer to that question r(4,t), is a long-standing Ramsey problem that has plagued the mathematical world for decades.

What’s Ramsay’s problem?

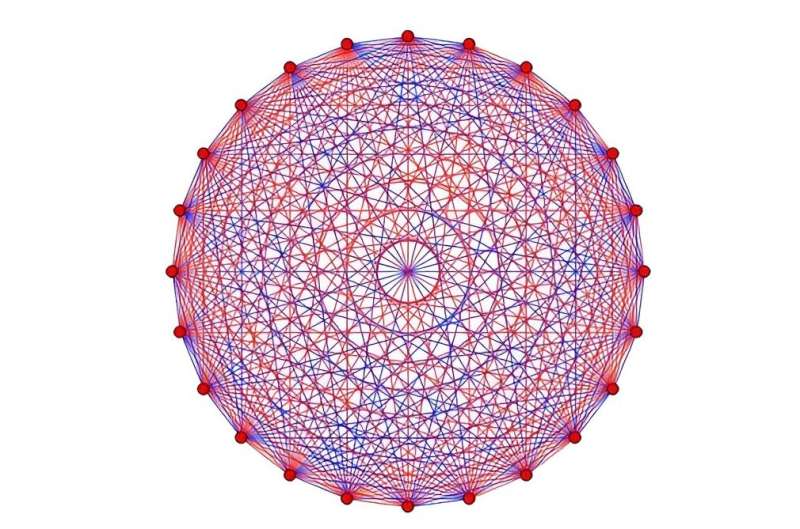
In mathematics, a graph is a series of points and lines between those points. Ramsey theorem states that if a graph is large enough, You’re guaranteed to find some kind of class Within it – either a set of points with no lines between them or a set of points with all possible lines between them (such sets are called “sets”). This is written as r(s,t) where s are the points with lines and t are the points without lines.

For those of us who are not interested in graph theory, the most common Ramsey problem is sometimes called r(3,3). “Friends and Strangers Theory” He explained through the party: In a group of six people, you will find at least three people who know each other or three people who do not know each other. The answer to r(3,3) is six.

“It is a fact of nature, an absolute truth. It does not matter the situation or which six people you choose – you will find three people who know each other or three people who do not know each other. You may be able to find more, but it is certain that there will be at least three in one group or the other” Verstreet said.

What happened After mathematicians found that r(3,3) = 6; Of course, they wanted to know r(4,4), r(5,5) and r(4,t) Where the number of disconnected points is variable. The solution for r(4,4) is 18 and is proven using a theory Created by Paul Erdos and George Sikiris in the 1930s.

currently P(5,5) is still unknown.

A good problem to resist

Why is something so simple to formulate so difficult to solve? It turns out that it’s more complicated than it seems. Let’s say you know that the solution for r(5,5) is somewhere between 40-50. If you start with 45 pips, there will be over 10,234 charts to consider.

“Since these numbers are difficult to find, mathematicians look for estimates. And that’s what Sam and I achieved in our recent work. How can we find not the exact answer, but the best estimate of what those Ramsey numbers might be?” Verstraete explains.

Mathematics students learn Ramsey problems early, so r(4,t) was on Verstraete’s mind for most of his career. In fact, he saw the problem printed for the first time in the book.”Erdös on Charts: His Legacy of Unsolved Problems“, written by two UC San Diego professors, Fan Zhong and the late Ron Graham. The problem is A case written by Erdos, who offered $250 to the first person who could solve it.

Pseudorandom graphs provided the solution

Many people have thought about r(4,t). It has been an open problem for over 90 years. But it wasn’t something that was at the forefront of my research. “Everyone knows it’s hard and everyone has tried to solve it, so if you don’t have a new idea, you’re unlikely to get anywhere,” Verstraete explained.

About four years ago, Verstraete was working on a different Ramsey problem with University of Illinois-Chicago mathematician Dhruv Maupay. together They discovered that Pseudorandom graphs They can enhance current knowledge of these ancient problems.

In 1937, Erdös discovered that The use of random graphs can give good lower bounds on Ramsey problems. What Verstraete and Maupay discovered is just that Sampling pseudorandom graphs often gives better bounds on Ramsey numbers than random graphs. These limits – the upper and lower limits of the potential response – are restrictive The range of estimates they can make. In other words, They were closer to the truth.

the 2019, To the delight of the mathematicianVerstraete and Mubayi used pseudorandom graphs to solve r(3,t).. However, Firststreet Struggle to create a pseudorandom graph that can help solve r(4,t).

He began to deal with different areas of mathematics other than combinatorics, e.g Finite geometry, algebra and probability. He eventually joined forces with Matthews, a postdoctoral researcher in his group whose background was in limited engineering.

“It turned out that the pseudorandom graph we needed could be found in Finite Engineering. Sam was the perfect person to come to us and help us build what we needed.” Verstreet said.

Once they had the pseudorandom graph, they still had many calculations to solve. It took nearly a year, but they finally realized they had the solution: r(4,t) is close to a cubic function of t. If you want a party where there will always be four people who know each other, or people who don’t know each other, you’ll need the following:³ (R in III) Persons present. There is a small asterisk (actually 0) because this is an estimate and not an exact answer. but R³ Very close to the exact answer.

The results are under review in the Annals of Mathematics. a The preprint has been uploaded to arXiv.

“It actually took us years to solve this problem. There were many times we stumbled and wondered if we would ever figure it out. But we must never give up, no matter how long it takes.” “It’s a lot of work,” said Verstraetti, who emphasized the importance of perseverance, which he often reminds his students. “If you find a problem difficult and you’re stuck, then it’s a good problem. No Fan Zhong A good problem he resists. “You can’t wait for him to reveal himself.”.

Verstraete knows that such stubborn determination is well rewarded: “Fan Zhong called me and said she owed me $250.”

source: FOXreport.gr

Where is the head of the starfish? Scientists have finally solved the mystery

One of humanity’s greatest mysteries has been solved – finding the “Lost Continent” of Argoland